实验任务简介
实验背景
本次实验需要利用 $MATLAB$ 和所学的图像处理相关知识,对一张输入的图片进行 Haar 小波变换及 Huffman 编码,以达到图片压缩的目的。
实验环境
实验操作系统环境为 Windows 10 ,$MATLAB$ 版本为 R2021b 。
实验思路
实验大致分为以下几步:图片补全、 Haar 小波变换、 Huffman 编码、编码数据保存、编码数据读取、 Huffman解码、Harr 小波逆变换、计算压缩率并显示压缩前后对比结果。
程序框架与技术细节
总体框架
程序大致框架为: main.m 为程序入口,为程序整体的流程; Haar.m 为 Haar 小波变换过程的函数; Huffman.m 为对小波变换结果进行 Huffman 编码的函数; Haar_Inv.m 为 Haar 小波变换逆过程的函数。程序运行流程如下:

各模块功能介绍
main.m
main.m 作为程序的入口,主要起到表示程序流程及调用各模块函数的作用,具体过程如下:弹出文件选择对话框读入待操作图片,将图片长宽拓展到最近的 $2^n$ 大小,调用 Haar 小波变换函数进行小波变换处理,将结果矩阵变为有符号整数,调用 Huffman 函数进行 Huffman 编码处理,保存数据文件,清空工作区变量,读取数据文件,利用内置函数进行 Huffman 解码操作,将矩阵结果变回原大小,调用 Haar_Inv 函数进行小波逆变换处理,计算压缩率,对比显示原图与压缩图,显示压缩率。
Haar.m
Haar.m 是 Haar 小波变换过程的函数,具体计算方法为利用变换矩阵与图像矩阵进行矩阵乘法。 4 $\times$ 4 和 8 $\times$ 8 的小波变换矩阵如下,依此类推 $2^n \times 2^n$ 的小波变换矩阵。 $$ H_4 = \left[ \begin{matrix} \frac14 & \frac14 & \frac14 & \frac14 \\ \frac14 & \frac14 & -\frac14 & -\frac14\\ \frac12 & -\frac12 & 0 & 0\\ 0 & 0 & \frac12 & -\frac12 \end{matrix} \right] \\ H_8 = \left[ \begin{matrix} \frac18 & \frac18 & \frac18 & \frac18 & \frac18 & \frac18 & \frac18 & \frac18\\ \frac18 & \frac18 & \frac18 & \frac18 & -\frac18 & -\frac18 & -\frac18 & -\frac18\\ \frac14 & \frac14 & -\frac14 & -\frac14 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & \frac14 & \frac14 & -\frac14 & -\frac14\\ \frac12 & -\frac12 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & \frac12 & -\frac12 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & \frac12 & -\frac12 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & \frac12 & -\frac12 \end{matrix} \right] $$ 函数计算过程如下:
-
获取图片矩阵大小 $[r, c, dim]$ 。
-
根据图片矩阵列数计算相应的小波变换矩阵 $H_c$。
-
用该小波变换矩阵与图片矩阵的转置矩阵进行矩阵乘法,然后再转置,即 $$ I = (H_c \times I^T)^T $$
-
根据图片矩阵行数计算相应的小波变换矩阵 $H_r$ 。
-
用该小波变换矩阵与图片矩阵进行矩阵乘法,得到小波变换最终结果,即 $$ I = H_r \times I $$
-
对结果矩阵进行阈值处理,在本程序中,绝对值小于等于 2 的部分将被舍弃为 0 。
Huffman.m
Huffman 函数的功能是对 Haar 小波变换完的矩阵进行 Huffman 编码,在函数中编码部分主要由 $MATLAB$ 内嵌函数完成,其余笔者自行编写的部分为对矩阵进行预处理的过程。
函数计算过程如下:
- 将小波变换完的矩阵乘上行列数以整数化。
- 分图层每层拉直为行向量。
- 计算每个元素出现的概率。
- 利用
huffmandict函数进行字典的生成。 - 利用
huffmanenco函数进行每一层的编码,并记录其编码长度。
Haar_Inv.m
Haar_Inv 函数是 Haar.m 函数的逆过程,即从 Haar 小波变换的结果矩阵还原回图像原始矩阵。4 $\times$ 4 和 8 $\times$ 8 的小波变换逆矩阵如下,依此类推 $2^n \times 2^n$ 大小的逆变换矩阵。 $$ H_{inv_4}= \left[ \begin{matrix} 1 & 1 & 1 & 0\\ 1 & 1 & -1 & 0\\ 1 & -1 & 0 & 1\\ 1 & -1 & 0 & -1 \end{matrix} \right] \\ H_{inv_8}= \left[ \begin{matrix} 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0\\ 1 & 1 & 1 & 0 & -1 & 0 & 0 & 0\\ 1 & 1 & -1 & 0 & 0 & 1 & 0 & 0\\ 1 & 1 & -1 & 0 & 0 & -1 & 0 & 0\\ 1 & -1 & 0 & 1 & 0 & 0 & 1 & 0\\ 1 & -1 & 0 & 1 & 0 & 0 & -1 & 0\\ 1 & -1 & 0 & -1 & 0 & 0 & 0 & 1\\ 1 & -1 & 0 & -1 & 0 & 0 & 0 & -1 \end{matrix} \right] $$ 函数计算过程如下:
-
获取图片矩阵大小 $[r, c, dim]$ 。
-
根据图片矩阵行数计算相应的小波变换矩阵 $H_{inv_r}$。
-
用该小波变换矩阵与图片矩阵的转置矩阵进行矩阵乘法,然后再转置,即 $$ I = H_{inv_r} \times I $$
-
根据图片矩阵行数计算相应的小波变换矩阵 $H_{inv_c}$ 。
-
用该小波变换矩阵与图片矩阵进行矩阵乘法,得到小波变换最终结果,即 $$ I = (H_{inv_c} \times I^T)^T $$
程序运行示例
运行说明
打开 $MATLAB$ 后,操作步骤如下:
- 将 src 目录设为 $MATLAB$ 当前文件夹。
- 在 $MATLAB$ 命令行窗口输入
main运行程序。 - 程序弹出文件选择对话框,选择一张图片(样例图片路径为 ./img/jiiku.jpg)。
- 等待程序进行编码、存储、解码,并最终弹出压缩前后对比图及压缩率。
运行结果示例
运行过程和结果示例如下:
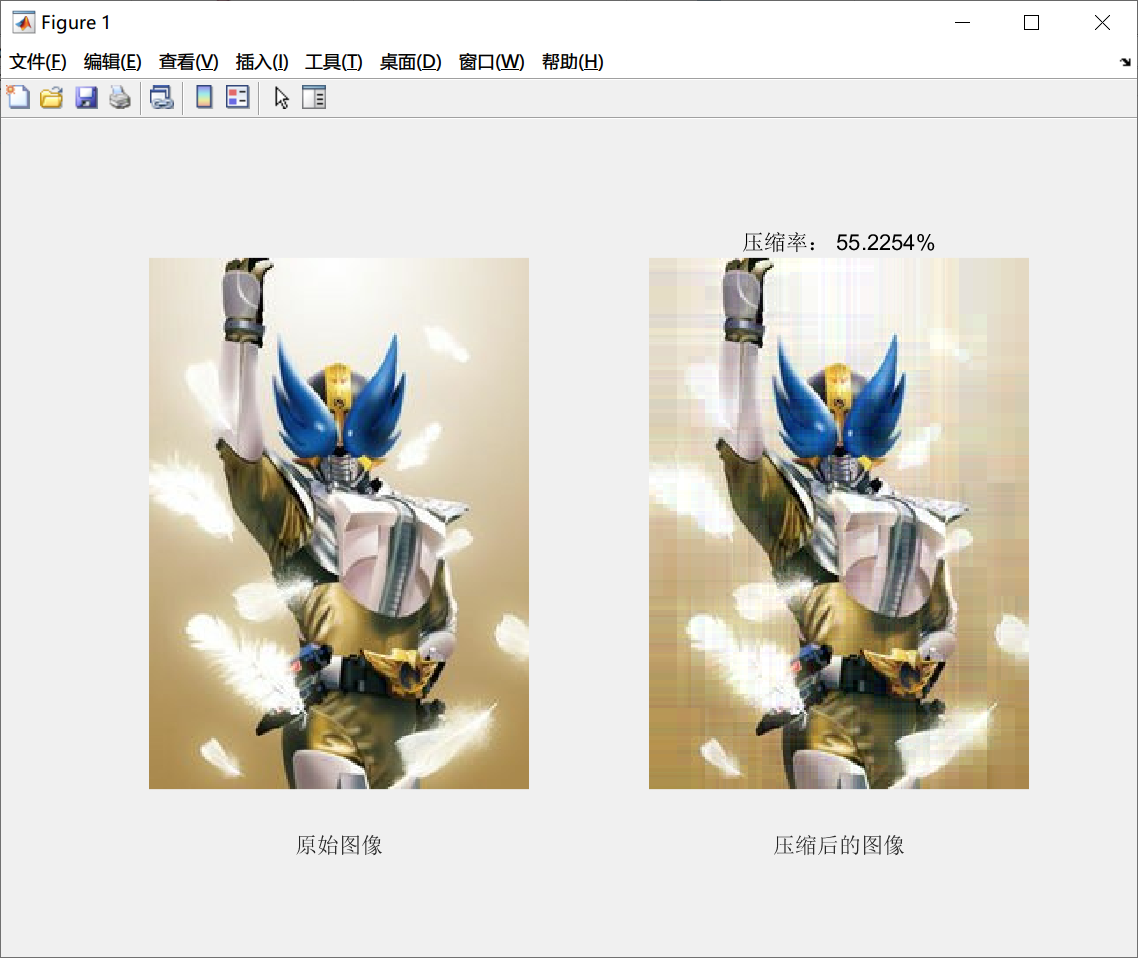
实验结果分析
实验结果展示
| 阈值 | 运行结果 | 运行时间 |
|---|---|---|
| 0.5 | 
|

|
| 1 | 
|

|
| 2 | 
|

|
| 5 | 
|

|
结果分析
| 阈值 | 压缩率 | 运行时间 |
|---|---|---|
| 0.5 | 79.7213% | 153.749 秒 |
| 1 | 68.045% | 149.281 秒 |
| 2 | 55.2254% | 87.212 秒 |
| 5 | 39.1632% | 58.992 秒 |
从结果中可以看到,随着 Haar 变换结果阈值的提高,程序运行速度逐渐变快,压缩率逐渐降低,但图像的质量也随之降低。因此在不同场合应用此算法时,需要根据场景需求来选择合适的阈值,才能达到最好的效果。